Join Detective IQ Club | Daily Riddles and Puzzles for Logical Minds

Join one of the top clubs for logical people! Detective IQ Club offers daily riddles and puzzles to challenge your mind and boost your IQ. Engage with a community of sharp thinkers and solve mysteries every day.

find-the-difference

Find differences between four friends

Que. 256

Find the Difference !

find the difference friends

  • 4
  • 5
  • 6
  • 7

    In the first image, the first boy has a bird on his head, but in the second image, it's not there. The second boy is on the left side in the first image, but in the second image, he is at the top. The boy in the yellow t-shirt is smiling in the first image, but not in the second one. In the first image, there is only a hockey stick, but in the second image, there is a ball along with the stick. The kite in the first image has only two flowers, while in the second image, it has three.
find-the-missing-piece

Missing Piece Puzzles

Que. 257

Find the missing piece !

find the missing piece puzzle

  • A
  • B
  • C
  • D
find-difference

Find the Difference puzzle

Que. 258

Find the Difference !

find-the-difference-dogs

  • 5
  • 6
  • 7
  • 8
find-the-difference

Find Difference Puzzle

Que. 259

Find the difference !

find the difference snail

  • 3
  • 4
  • 5
  • 6
which-number-replaces-the-unknown

Which Number Replaces the Unknown?

Que. 260

Which number comes into your mind to replace unknown?

missing number triangle puzzle

  • 6
  • 7
  • 8
  • 9
can-you-solve-this-duck-dog-rabbit-math-equation

Solve This Duck Dog Rabbit Math Equation?

Que. 261

Can you solve this Duck dog rabbit math equation?

duck rabbit dog puzzle

  • 54
  • 27
  • 24

    AA all the 3 equations so you will get 
    2 duck + 2 Dog + 2 rabbit equals 54

    so divide by 2
    1 duck + 11 dog + 1 rabbit equals 27
solve-this-math-equation-2-2-2

Math Equation

Que. 262

Can you solve this?


2 2 2 equation puzzle

  • 8
  • 6
  • 4
  • 10
how-many-triangles

How many triangles puzzles

Que. 263

How many triangles?


how many triangles

  • 9
  • 13
  • 11
  • 15

    There are 13 triangles
find-the-missing-number

Missing Number puzzle

Que. 264

Find the missing number?

ind the missing number

  • 6
  • 5
  • 7
  • 4
how-many-cubes-are-there

How Many Cubes puzzle

Que. 265

How many cubes are there?

how many cubes are there

  • 7
  • 10
  • 8
  • 9

    The total number of cubes is 9.
which-switch-will-turn-on-the-light

swtich puzzle

Que. 266

Which switch will turn on light?

which switch will turn on liht

  • Yellow
  • Green
  • Red
  • Purple
help-the-bee-find-its-path

Find the Path!

Que. 267

Help the bee to find its path!

help the bee to find its path

  • 1
  • 2
  • 3
  • 4

    The correct path for the bee is 4 because it leads to the destination without obstacles or dead ends. The other paths likely contain obstacles or incorrect routes.
find-the-back-side-view-puzzle

Back Side View puzzle

Que. 268

Find the back side view?

find the back side view pencil puzzle

  • A
  • B
  • C
  • D

    The correct answer is B because it accurately shows the back side view of the pencil arrangement.
how-many-small-cubes-to-fill-the-space

How Many Cubes Are Needed?

Que. 269

How many small cubes do you need to fill the empty spaces?


how many small cubes do you need to fill the empty space

  • 24
  • 23
  • 27
  • 28

    23 is the right answer
    Total cubes for this area will be 9x3=27
    4 cubes already present (4th below 1)

    so 27-4=23 
move-one-matchstick-equation-puzzle

Move one matchstick equation puzzle

Que. 270

Move one matchstick to Fix the equation 9-8=2

detective iq club image 9

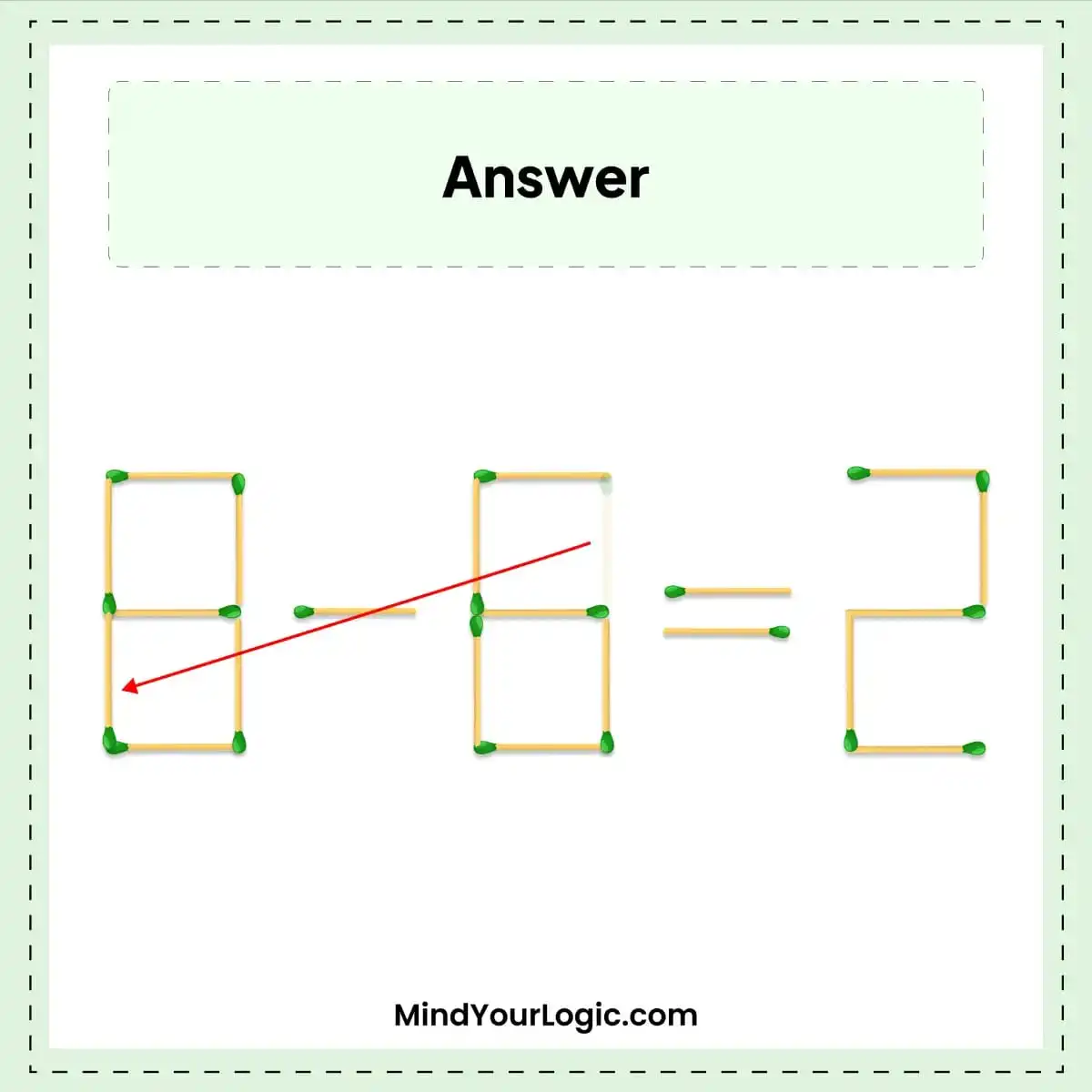
    8 6 2 mathstick equation answer

     

    Solving the matchstick puzzle 9-8=2 is as simple as moving just one matchstick to create a valid math equation.


    Start with the original equation: 9-8=2.

    Take one of the matchsticks from the number 8.

    Place the matchstick you removed from 8 into the number 9, turning it into an 8.

    So the 8 becomes 6 and 9 becomes 8

    Your equation now reads 8-6=2.